2011-01-04

グラフのはなし

今日は昨日までと話題を変えてグラフの話をします.
でも順序の話とつながっている話なのです.
どうつながっているかは追々.

グラフとは?

グラフと聞くと y = f(x) を xy 平面に書いたものを思い浮かべる人がいるかもしれませんが, ここで言うグラフはそのグラフとは異なります. (両方ともグラフと言うからややこしいんですが……)

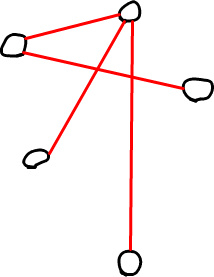
逆にソーシャルグラフのグラフはここで言うグラフと同じ意味です. 人物相関図のような点 (ソーシャルグラフでは人物) がたくさんあり, それらが線 (関係) で結ばれているものをグラフと呼びます.

イメージとしてはこんな感じです.

この図では点どうしが線で結ばれていますが, 矢印で結ばれることもあります.

数学の言葉では, 点は「節 (node, vertex)」と言い, 線 (矢印) は「辺 (edge)」などと言います. (が, このシリーズではあまり学術用語は重視しませんので, 忘れてしまっても問題ありません.)

グラフの例

グラフの例はさっきの人物相関図などのように日常的にありふれたものでしょう.

何かと何かが関係していてその関係が言葉だけでは表せないとき, そこにグラフが出てくるはずです.
家系図然り, (モンハンなどの) ゲームのマップ然り.
きっと何らかの理由付けがあって人間の思考に馴染む表現形式なのでしょう.

順序との関係

あるグラフがあったときに, そのグラフの点を一列に並べたい場合があります. 一列に並べるということは, グラフの点たちに順序を付ける, ということで順序が登場してきますね. (ふぅ, これを言うのにだいぶかかった.)

明日以降はグラフの点の順序付けの話をしていこうと思います.

それでは.

あとがき

ちょっと今日はパワー不足で短めになってしまいました.

もしここまで読んでくれている方がいたら, Twitter で一言でいいので声を掛けていただけると有難いです. 喜びます. → http://twitter.com/cocoatomo

2011-01-03

順序のはなし・その3

math ComputerScience order

今日扱うのは「前順序」(preorder) です. (しつこいようですが「全順序」の typo ではないです.)

私の事情で今日は短めにします. 細かいところは端折りますが内容は漏らさずに書くので, 質問などあればコメントや Twitter ( http://twitter.com/cocoatomo ) の方へお気軽にどうぞ.

前順序の定義

さていつも通り定義から入りましょう.

どんな a でも a ≦ a
a ≦ b かつ b ≦ c ならば a ≦ c

昨日の「半順序」から2つ目のルールが消えている形ですね.「a ≦ b かつ a ≧ b でも a = b とは言えない」という性質の順序です.「全順序」よりも弱い「半順序」と比べてさらに弱い順序ということですね.

前順序の例

かなり条件の緩い順序なので, いい加減な比較をしている例を出せば良いことになります.

例えばグループごとの人数で順序付けをする場合,「5人のグループの方が4人のグループよりも大きい」ということは言えますが,「どちらのグループも5人のグループだから同じグループだ」と言うのは違和感がありますね.

グループのメンバーが異っているのにそれらを一緒くたに扱うところに違和感があるのでしょう.「グループの人数」という観点のみで比較しているため,「グループのメンバー」という細かいところまで把握できていないのです. こういう「大雑把な比較」が前順序です.

明日以降

さて, 最初に挙げたネタが尽きたわけですが, 順序に絡めてグラフの話をしていこうと思います.「BFS」「DFS」「topological sort」あたりを取り上げる予定です.

「圏と絡めた順序の話とかも紹介できたらいいなぁ」とも思ってますが, 自分の勉強のペース次第です^-^;

おまけ

最近, 太郎の「男女」が「順序」の歌にしか聞こえません.

♪先生, 男子が列を乱して並びません
先生, 女子がおしゃれな順序でもめています

うるさい, 並べ, 整列結果を乱すな

2011-01-02

順序のはなし・その2

math ComputerScience order

さて今日は「半順序」の話をします.
昨日の全順序 (total order) に比べやや足りないところがあるので,「半順序」(partial order) と言います. どこが足りないかをこれから見ていきましょう.

半順序の定義

さて, まずは定義から行きましょう. 全順序のときと同じように記号「≦」が満たすルールを並べて定義します.

どんな a でも a ≦ a
a ≦ b かつ b ≦ a ならば a = b
a ≦ b かつ b ≦ c ならば a ≦ c

昨日の全順序と比べてどこが違うでしょうか?

そうです, 1つ目のルール以外は全く一緒です. そして, 全順序の1つ目のルール「a ≦ b または b ≦ a が成立する」から b が a だった場合を考えると,「a ≦ a」が出てきます. 今何を示したかというと, 全順序の1つ目のルールから半順序の1つ目のルールが導き出せることを示しました.

その逆はどうなるかと言うと導き出すことはできません. つまり全順序のルールは半順序のルールよりも強い (別の言い方だと「厳しい」) ものなのです. ここに全順序と半順序の違いがあります.

全順序の1つ目のルールが何を言っていたかと言うと,「a ≦ b または b ≦ a」つまり「どんな2つのものでも比較できる」ということでした. 半順序では「自分自身とは比較できる」ということしか保証されていません. この性質が足りないことを指して「半」(partial) という名前なのだと思います.

半順序の例

さて, 昨日扱った「全順序」は「順序」と呼ぶに相応しい感じがしましたが, 今日の「半順序」にはどんな例があるのでしょうか? 果たして自然な例はあるのでしょうか?

私はある集団を考えたときに, そこに入る順序はほとんどは「半順序」で「全順序」は無理矢理付けないと付けられない序列だと思っています.

例えば, とある試験の5教科の成績があったときにそれ比較するときのことを考えてみましょう.

A 君は「国語: 50, 数学: 100, 理科: 80, 社会: 60, 英語: 60」B 君は「国語: 80, 数学: 70, 理科 50, 社会: 70, 英語: 70」という成績だったとします. さて2人のうち「成績が良い」方はどちらでしょうか?

良くある評価方法は合計点で競う方法です. A 君は合計点 350 点, B 君は合計点 340 点なので A 君の方が成績が良いと言うことができます.

他には教科ごとに点数を比較する方法があります. A 君は2勝 (数学, 理科) B 君は3勝 (国語, 社会, 英語) なので, この観点では Β 君の方が成績が良いと言えます.

しかしどちらもあまり釈然としないところが残らないでしょうか?
合計点で競っても,「国語の1点」と「数学の1点」は本当に同じものなのでしょうか? 単純に足してしまって良いのでしょうか? また教科ごとの勝敗で見ても大差で勝っているものもあれば, 僅差で負けているものもあります. そんな状況でそれらを同じ1勝として数えて良いのでしょうか?

ここで全て100点だった人 (C 君) がいれば比較は簡単ですよね? その人はどんな人と比べても, 同じかより成績が良いと言えます.

ここに「半順序」が現れているのです. 1つ目のルールで全順序に対し欠けているのは比較可能性でした. 別の言い方をすると「ある2つのものが比較できないこともある」ということです. 上の例では5教科の成績というものに無理矢理全順序を入れようとしたためやや不自然な順序が入りましたが,「そもそも全順序を入れるのがおかしい」と考える考え方も有りです.

そこで半順序です.「A 君が B 君に対し全ての教科において同じか負けているときに A ≦ B」と定義すれば, これは半順序のルール (公理) を満たします. さすがにこのルールで順序を付ければ文句は無いでしょう.

さて, 今日はこれくらいにします. 順序のイメージが付いてきたでしょうか?
明日は「前順序」(全順序の typo ではない) を扱います.

それでは.

おまけ

順序の例として学校が舞台に上がるのは偶然なのでしょうか. (反語)

余談

このネタは @kinaba さんのブログの正規表現しちへんげ！シリーズだったり, @alg_d さんの一連のつぶやきに刺激されて書いています.

2011-01-01

順序のはなし

math ComputerScience order

古来より日本のプログラマの間には、「正月はフラクタル」という風習があります。
http://d.hatena.ne.jp/ku-ma-me/20110101/p1

ほぉ〜寡聞にして知らなんだ。

じゃあ、俺は「正月は数学」という風習を始めてみようと思います。

よしっ、今年のテーマは「順序 (ordering)」。順序に関わる話題を1ヶ月続けてみます。
「大学数学に興味があるけれどどう勉強していいか分からない。とっかかりが欲しい。」という人を対象に、平易なところから始めてみることにします。

全順序 (total order) の定義

最初は各順序の定義から始めます。

順序には色んな種類があるのでまず全順序から話をしていきます。
この順序は普段使っている「順序」のことで、どんな2つのものに対して大小が付けられるものを言います。

順序を記号で「a ≦ b」と書いて、「a は b 以下」と読みます。

定義の形で書くと、以下の3つのルール (公理) を満たすものとなります。

~~どんな a でも a ≦ a~~ どんな a, b でも a ≦ b または a ≧ b のどちらかが成り立つ
a ≦ b かつ b ≦ a ならば a = b
a ≦ b かつ b ≦ c ならば a ≦ c

どれも当たり前のことを言ってると思いますが、それを改めてルールとして抽出するのが重要なのです。
ある命題を示すときには、この抽出したルールのみを使って証明を進めていきます。

余談

「<」じゃなく「≦」を使うのはなぜか? と思われたかもしれませんが、特に大きな意味は無いと思います。
上記の全順序に対して「<」を「≦ かつ ≠」と定義できます。そして、逆に

a < b, a = b, a > b のどれか1つのみ成立する
a < b かつ b < c ならば a < c

と「より小さい」ことを定義して、「≦」を「< または =」と別の定義を与えることができます。
(「『=』の定義は何だ!?」というツッコミは確かにあるのですが、今回は「順序」シリーズなので同値に関してはまた別のシリーズで扱いたいと思います。
ひとまず、普通にイメージする等号「=」と思ってください。)

こうやって「<」を経由して「≦」を定義することができ、当然最初に出した定義と同じことを言ってます。

ちょっとそれを確かめてみましょう。さて、何を示せば良いのでしょうか?

定義が同じことを言うには、片方の定義に出てくるルール (公理) からもう一方の定義のルール (この場合は気分的には「命題」と読んだりしたいです。) が成り立っていることを示せば良いです。
つまり、「<」が上のように定義されているとき「≦」=「< または =」についての3つの命題を示します。

~~どんな a でも「a = a」は成立しているので、「a < a または a = a」も成立しています。~~ a < b, a = b, a > b のどれかが成立しているので, a ≦ b または a ≧ b のどちらかが成り立ちます.
「「a < b または a = b」かつ「a > b または a = b」」を変形すると「「a < b かつ a > b」または「a < b かつ a = b」または「a = b かつ a > b」または「a = b かつ a = b」」となり、定義より a < b, a = b, a > b のどれか1つのみ成立するので「a = b」が成立することが分かります。(この変形はいわゆる分配法則です。)
「「a < b または a = b」かつ「b < c または b = c」」を変形すると「「a < b かつ b < c」または「a < b かつ b = c」または「a = b かつ b < c」または「a = b かつ b = c」」となり、まとめると「a < c または a < c または a < c または a = c」つまり「a ≦ c」となって欲しかった結論が出ます。

定義が同等である、ということのイメージが付いたでしょうか?
こういう議論はある程度の慣れが必要かと思いますので、何度も考えてみてください。

全順序の例

さて余談が長くなりましたが、本筋に戻って全順序が出てくる例を見ていきます。

まず自然数 (ここでは正の整数、1、2、3… とします) には全順序が出てきます。
通常の意味での大小関係があり、上の「≦」が満たすべきルール (公理) を満たしているので自然数には全順序があります。
(より正確に言うと「自然数は通常の大小関係が全順序となる集合」のような表現になるのですが、ここでは敢えて端折った不正確な表現をしています。)

次に整数 (0、±1、±2…) を考えてみましょう。
これにもさっきの自然数と同じく通常の意味での大小関係が全順序となります。

自然数と大きく違うところは整数には最小元はありません。自然数には「1」という「一番小さい数」がありますが、
整数では常にどんな数にもそれより小さい数 (例えば1つ小さい数) が存在して底無しに続いていきます。
この特徴は後で無限降下法を扱うところで効いてくるので、覚えておいてください。(そして俺も書くのを忘れないようにします!)

ちょっと複雑な例を出しましょう。
文字列の辞書順について見てみましょう。

辞書順とは「先頭の文字から比較していって50音順で早いものが前の方に、同じだった場合は次の文字で比較。さらに同じだったらさらに次の文字へ。」という比較の仕方でしたね。「は」と「ば」など細かいところに関しては今は解説は省きます。

当然、辞書は単語を辞書順で並べています。また学校の出席番号も姓名に関する辞書順です。
(私のときは男女別に番号を振っていたが、今は男女一緒に番号を振ったりするのだろうか?)

そしてこの並べ方だとどっちの出席番号がより後ろに来るのかはっきり決まります。
「こっちの人が前だけれど、考えようによっては別の人の方が前」というような曖昧さはありません。
この順序に関して曖昧さが無い、というのは別の言い方をすれば「1列に並べられる」ということです。
ここが「全順序」の特徴が強く出ているところなので、よく意識に焼き付けておいてください。

小学校の算数や国語の授業中は出席番号順に並んで勉強することが (特に新学年が始まった頃は) ありますが、体育の時間はまた別の順序で並びますね?
そうです「身長順」です。同じ集団に2つ以上の順序が入ることがあるのです。

これは裏を返せば、「ある集団 (集合) には好きに全順序が入れられる」ということです。もちろん上記の定義の3つの公理 (ルール) を守っている必要はありますが。

なので「誕生日の早い順」だったり「住所の辞書順」だったり色々な順序を作ることができます。順序はただ与えられるものではなく自分で定義できるものなのです。

明日以降は「半順序」「前順序」について扱っていきます。

おまけ

ただの思い付きです。

♪順序全順序順序、順序半順序順序、順序前順序ポセット順序、序順序順序最小元
(ポセット (poset) とかについては今後扱っていきます。)

2009-07-18

21問目

Project Euler math

$d(n)$ を真の約数( $n$ の約数のうち $n$ より真に小さいもの)の合計と定義する.
もし $d(a)=b$ かつ $d(b)=a$ であり $a\neq b$ の場合, $a$ と $b$ を友愛数と呼ぶ.
例えば, 220 の真の約数は 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110 なので $d(220)=284$ . 284 の真の約数は 1, 2, 4, 71, 142 なので $d(284)=220$ .
10000 未満の全ての友愛数の合計を求めよ.
http://projecteuler.net/index.php?section=problems&id=21

友愛数っていうのは, 代数学やってた身としては親しみのある数学の対象なのですが, 如何せん「約数を足す」という掛け算に関わる数字を足す操作をしてしまうため, なんとも扱いづらい数字なのです. 問題の理解のしやすさと解決の難しさの乖離という点では, 14問目の Collatz の問題と似た感じです.

このプログラムでもバリバリ素数を使っているので, やっぱり自作の prime 関数を使っています. prime 関数の実装が見たい人は過去の日記などを探してください. そのうちホームページの方にも載せます.

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "prime.h"

int sumOfDivisors(int);
int sumOfProperDivisors(int);
int solveVer00(int);

int main(int argc, char **argv) {
	int upperBound;

	if (argc < 2) {
		fprintf(stderr, "Error: too few argument.\n"
				"a value of upper bound is needed.\n");
		return EXIT_FAILURE;
	}

	upperBound = atoi(argv[1]);
	fprintf(stdout, "Solution: %d.\n", solveVer00(upperBound));

	return EXIT_SUCCESS;
}

int solveVer00(int upperBound) {
	int number;
	int companion;
	int result;

	initPrime();
	for (number = 2, result = 0; number < upperBound; number++) {
		companion = sumOfProperDivisors(number);
		if (number != companion
			&& number == sumOfProperDivisors(companion)) {
			result += number;
//			fprintf(stdout, "%d, %d\n", number, companion);
		}
	}

	return result;
}

int sumOfProperDivisors(int number) {
	return sumOfDivisors(number) - number;
}

int sumOfDivisors(int number) {
	long long p;
	int power;
	int result;

	prime(-1);
	result = 1;
	while (number > 1
		   && (p = prime(0)) != -1) {
		power = 0;
		while ((number % p) == 0) {
			number /= p;
			power++;
		}
		result *= (pow(p, power + 1) - 1) / (p - 1);
	}

	return result;
}

2009-07-18

19問目

Project Euler math

以下のような情報があります. また, 各自で調査しても良いでしょう.

1900年1月1日は月曜日.

小の月は9月, 4月, 6月, 11月. 残りは2月を除いて大の月. 2月は通常は28日だが, 閏年では29日.

閏年は, 4年に1度あり, 100年に1度は閏年でなくなり, さらに400年に1度は閏年になる.

20世紀(1901年1月1日から2000年12月31日)にはいくつの1日が日曜日になるか?
http://projecteuler.net/index.php?section=problems&id=19

問題とは関係無いが, ソースを書いていて気付いたのは, 「朔日」(ついたち)に当たる英単語が無いこと. ユリウス暦もグレゴリオ暦も太陽暦に分類されるからなのかなぁ?

さてこの問題では, 例外を含む周期的な数列の数え上げをどうコーディングするか?というのがテーマでした. 20世紀をある単位の繰り返しに分割し, その1周期の「最初の曜日」とその1周期の間での「1日の日曜日の数」の関係を配列に持っておいて, 次の周期との曜日のずれを計算しつつ1日の日曜日の合計を求めるという方針で行きました.
周期の候補としては1年, 4年, 100年, 400年という4種類の周期が考えられますが, 人間に分かりやすいということから1年を採用しました. 4年ごとにしても良かったのですが, 上記の配列の意味が分かりづらくなるので止めました.

#include <stdio.h>
#include <stdlib.h>

enum day {sun, mon, tue, wed, thu, fri, sat};
const enum day JAN_1st_1901 = tue;
const int N_DAYS_IN_YEAR = 365;
const int N_DAYS_IN_LEAP_YEAR = 366;
#define N_DAYS_IN_WEEK 7
/*
 * differences January 1st and the first day in each month.
 */
const int firstDays[N_DAYS_IN_WEEK] = {2, 1, 1, 3, 1, 2, 2};
const int firstDaysInLeapYear[N_DAYS_IN_WEEK] = {3, 1, 1, 2, 2, 1, 2};

const int FIRST_YEAR_IN_19TH_CENTURY = 1901;
const int FIRST_YEAR_IN_20TH_CENTURY = 2001;

int solveVer00();
int isLeapYear(int);
enum day nextNewYearsDay(int, enum day);
int numOfFirstDaysOfSunday(int year, enum day newYearsDay);

int main() {
	fprintf(stdout, "Solution: %d.\n", solveVer00());
	return EXIT_SUCCESS;
}

int solveVer00() {
	int result;
	int year;
	enum day newYearsDay;

	for (year = FIRST_YEAR_IN_19TH_CENTURY, newYearsDay = JAN_1st_1901, result = 0;
		 year < FIRST_YEAR_IN_20TH_CENTURY;
		 newYearsDay = nextNewYearsDay(year, newYearsDay), year++) {
		result += numOfFirstDaysOfSunday(year, newYearsDay);
	}

	return result;
}

int numOfFirstDaysOfSunday(int year, enum day newYearsDay) {
		if (isLeapYear(year)) {
			return firstDaysInLeapYear[(N_DAYS_IN_WEEK - newYearsDay) % N_DAYS_IN_WEEK];
		} else {
			return firstDays[(N_DAYS_IN_WEEK - newYearsDay) % N_DAYS_IN_WEEK];
		}	
}

int isLeapYear(int year) {
	return year % 4 == 0 && (year % 100 != 0 || year % 400 == 0);
}

enum day nextNewYearsDay(int year, enum day thisYears) {
	if (isLeapYear(year)) {
		return (thisYears + N_DAYS_IN_LEAP_YEAR) % N_DAYS_IN_WEEK;
	} else {
		return (thisYears + N_DAYS_IN_YEAR) % N_DAYS_IN_WEEK;
	}
}

2009-07-18

17問目

Project Euler math

数字の1から5までを単語で書くと one, two, three, four, five となり, 全部で3+3+5+4+4=19文字使っています.
では, 1から1000(one thousand)までを単語で書くと何文字使うでしょうか?
メモ: ハイフンや空白は数に数えません. 例えば, 342 (three hundred and forty-two) は23文字で書かれ, 115 (one hundred and fifteen) は20文字で書かれています. また, 数を書くときの "and" の使い方はイギリス式とします.
http://projecteuler.net/index.php?section=problems&id=17

まず「イギリス式」って何?( ﾟдﾟ)ﾎﾟｶｰﾝ
とりあえず中学のときに習った方法でいいんだよね?
まぁ, もうほとんど忘れてるので, ネットで調べましたが(-_-;

てか, 英語の数詞ってけっこう例外があるんだな. 日本語の数詞の方がよほど規則的だぞ, と.
結局, この問題は気合いで数え上げて正解しました. 工夫なんてなくただ丁寧に数え上げただけ. あんま面白くなかったな.